Projects/Research

• Applications of Finite Sets
  This is Jeremy Knight's presentation link for the T.A.M.U. final oral exam for the Masters of Mathematics.
• Finite Element Method and the Poisson Problem
  This is a link to web-pages, papers, and algorithms that I wrote to explain and demonstrate the use of applying the Finite Element Method to finding solutions of the Poisson Problem.
  
• Numerical Solutions of the Navier-Stokes Equations.
  This is a project that I am currently developing to create a rigorous Matlab algorithm for finding numerical solutions to the Navier-Stokes equations at low Raleigh's numbers.
• Three Body Problem
  The three body problem is a dynamical system problem modeling the chaotic path of three orbiting bodies affected by Newton's laws of gravity.
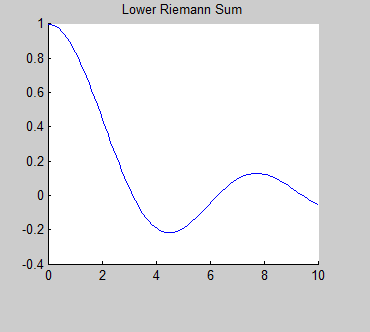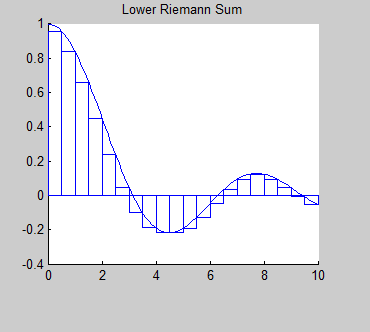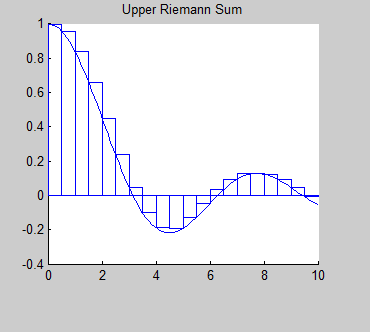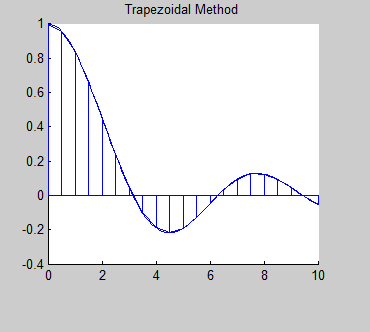
• Introduction to Rieman Sums
  A lesson for students to learn about the Riemann sums and explore them using RiemannSums2.m which produces the plot shown to the right.

Iterative and Numerical Methods

The following Maple algorithms employ iterative algorithms to acquire numerical approximations.

General algorithms

• Mini-Algorithms - a collection of short algorithms for incorporating into larger programs
• Jacobian - compute the Jacobian matrix
• L2 Norm

Approximations for roots and solutions to systems of equations

• Newton's Method for finding roots.
• Newton's Method for Minimum
• Fixed Point
• Broyden's Method
• Method of Steepest Descdent
• Gauss-Siedel method for solving systems
• SOR (successive over-relaxation) method
• Power method
• Symmetric Power method
• Inverse Power method
• Wielandt method
• Householder method
• QR method
• Jacobi Iterative method for systems (relative norm)
• Jacobi Iterative method for systems (non-relative norm)
• SVD - singular value decomposition

Differentiation and Integration Algorithms

• Implicit Trapezoidal method

Differential Equation Algorithms

• Linear Shooting Method
• Nonlinear Shooting Method
• Linear Finite Difference
• Nonlinear Finite Difference
• Linear Rayleigh Ritz method
• Runge Kutta Method

Partial Differential Equation Algorithms

• Poisson Finite Difference
• Heat Equation Backward Difference
• Crank Nicholson Method
• Wave Equation Finite Difference

Cryptography

The following are Maple algorithms used for cryptography applications

• Euclidean Algorithm
• Extended Euclidean Algorithm
• Crypto - a simple algorithm for
• M-R Test
• Random Prime - generates a large prime number of given length.
• AKS primality test

Fractal Cryptography project

• Fractal Cryptography write up
• Fractal Cryptography algorithm

Chaos and Dynamical Systems

Projects(pdf):

• Dynamic Growth of the Tribolium Beetle Population
  Analyzing the sensitive dependence on initial conditions of an insect population.
  
• 3-body problem
  Analyzing the chaotic behavior of 3 bodies in space whose orbit is affected by the combined gravitational pull.

The following are Matlab algor

ithms for applications in dynamical systems and chaos problems.

• mandleset.m - plots the Mandelbrot set for a given function f(z).
  Begin by using function handle to enter function such as the standard f(z)=z^2+c which can be entered into Matlab using
  f(z,c)=@(z,c) z^2+c.
• threebody_script.m ; threebody.m - plots the path of the 3-body problem described above.
  Download both files to the same directory and run threebody_script.m. The second file contains the ODEs.
  Example plot to the right.
• twobody_script.m ; twobody.m - plots the path of two bodies in space affected by gravitational pull.
  Download both files to the same directory and run twobody_script.m. The second file contains the ODEs.
  Example: twobody_script(100,[-.35,.5,.25,-.5],1e-2)
  
• lyapunov.m - calculates the Lyapunov exponent for a given set of 1-dimensional data to determine the chaotic nature of the data.
  

Other Matlab

• Function Transformation GUI
  A great tool for demonstrating how function families transform.
  transform.m - transform.fig - Download both